Linear Regression

Basic Formula

The basic linear model is of the form:

\[ \hat{y} = b_0 + b_1 x \]

This should be immediately recognisable as a simple linear formula.

• \(x\) is the independent variable
• \(y\) is the dependent variable
• \(b_0\) is the \(y\) intercept
• \(b_1\) is the slope of the line.

Least Squares Function

Attempts to create a regression line by summing the distances between each point and the line. This is the error.

We run this function on many possible lines and choose the one that is lowest.

General Model - Multiple Linear Regression

Formally, we say we have an unknown function \(t = f(x)\), and a set of samples \(\{(x_i,t_i)\}\)

We use Multiple Linear Regression in the form of the set \(W\) where \(|W| = M\). This is a generalisation for linear regression, and can be easily used with no additional data, where \(M = 0\)

\[ \displaylines{ y(x,w) = x_0 + w_1 x_1 + w_2 x_2 + \dots + w_M x_M\\ = x_0 + \sum_{i=1}^M w_ix_i } \]

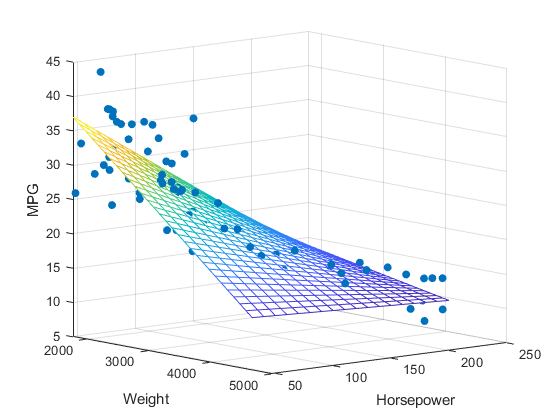
We can say each value \(w_i\) is a weight in our machine learning model.

Important: Each \(i\) in \(x_i\) represents a new dimension. So each dimension has an \(x\) input, and a \(w\) weight that determines the slope of that dimension.

Example - House Price Calculator

In the above video, there is an example of a 4-input dataset to calculate house prices. They use:

1. Square Metres of House
2. Number of Floors
3. Age
4. Number of Bedrooms

These values represent \(x_1, x_2, x_3,\) and \(x_4\) respectively, and the weights \(w_1\) to \(w_4\) will be given along with these inputs.

For example, if the number of bedrooms drastically affects the house price, then the value of \(w_4\) should be large in comparison to the rest of the values of \(W\).

Basis Functions

We can expand on the general model by also introducing a basis function \(\phi_i(x)\) to modify \(x\) in a simple regression:

\[ \displaylines{ y(x,w) = w_0 + w_1 \phi_1(x) + w_2 \phi_2(x) + \dots + w_M \phi_M(x) \\ = w_0 + \sum_{i=1}^M w_i \phi_i(x) } \]

This allows us to use non-linear regression lines. For example, polynomial or sigmoid.

Important: The multiplication of weights \(w\) is still linear, and these are the values we shall adjust. What isn’t linear is \(\phi(x)\), as this can be used to represent any non-linear function, as seen below.

This can be applied to our Generalised Model by making \(j\) the number of inputs. We then run this \(y\) function for all \(x_j\):

\[ y(x_j,w) = w_0 + \sum_{i=1}^M w_i \phi_i(x_j) \]

Examples of Basis Function

• Polynomial: \(\phi_i(x) = x^i\)
• Gaussian: \(\phi_i(x) = \text{exp}(-\frac{(x - \mu_i)^2}{2s^2})\)
• Sigmoid: \[ \displaylines{ \phi_i(x) = \sigma_{u,s} = \sigma \Big\lparen \frac{x - \mu}{s} \Big\rparen\\ \sigma(\alpha) = \frac{1}{1 + e^{-\alpha}} } \]

In the sigmoid function, \(\mu\) represents when the value is 0.5, while \(s\) represents the slope of the function.

Glossary

• Linear Regression: Calculation of a line that intercepts points on a graph with minimised error.
• Linear Model: A function that represents a linear regression.
• Multiple Linear Regression: Using multiple independent variables in a linear model.