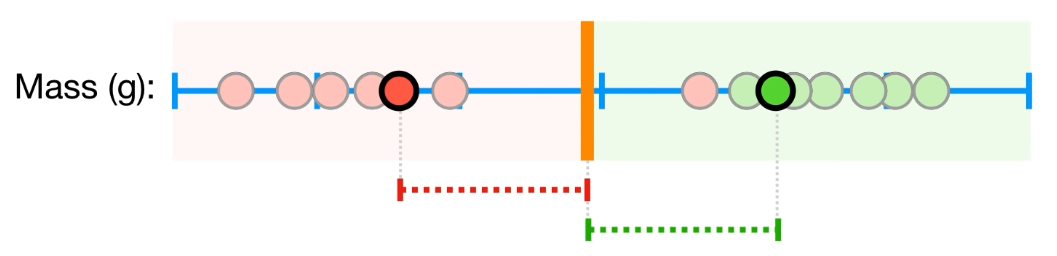
Classifiers divide a sample space using a line or plane, classifying data that appears on one side as class A, and data that appears on the other as class B.
Classifiers are calculated by taking the largest margin between two given data points. The choice of data points is important:

A support vector classifier uses a type of classifier called the Soft Margin. Observations within the soft margin can be misclassified. In the above example, the red point on the green side is within the soft margin, so misclassification is allowed. A soft margin is created using slack variables
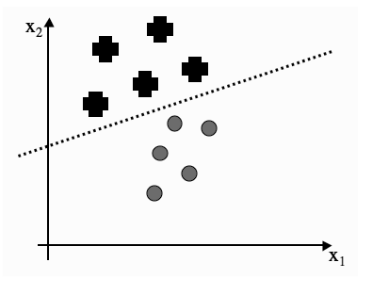
In the above example, the dotted line represents the SVC, classifying dots from plusses.
To make a prediction for a new data point \(z\), we use the equation:
\[ w^{*T}z + b^* = \Bigg(\sum_{i=1}^{n} \lambda_i t_i x_i\Bigg)^T z+b^* \]
We are computing the inner product between the new datapoint and the support vectors.
A Support Vector Machine tries classify data that is not linearly separable.
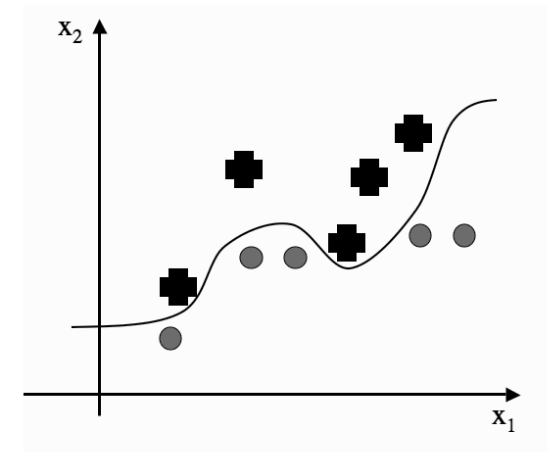
We do this by creating a kernel function \(\phi(x)\).
For a new data point \(z\), we create a kernel function \(\phi(z)\), and for every given data \(x_i\), we create a kernel function \(\phi(x_i)\). We can then plug this into the above equation:
\[ w^{*T}x + b^* = \Bigg(\sum_{i=1}^{n} \lambda_i t_i \phi(x_i)\Bigg)^T \phi(z)+b^* \]
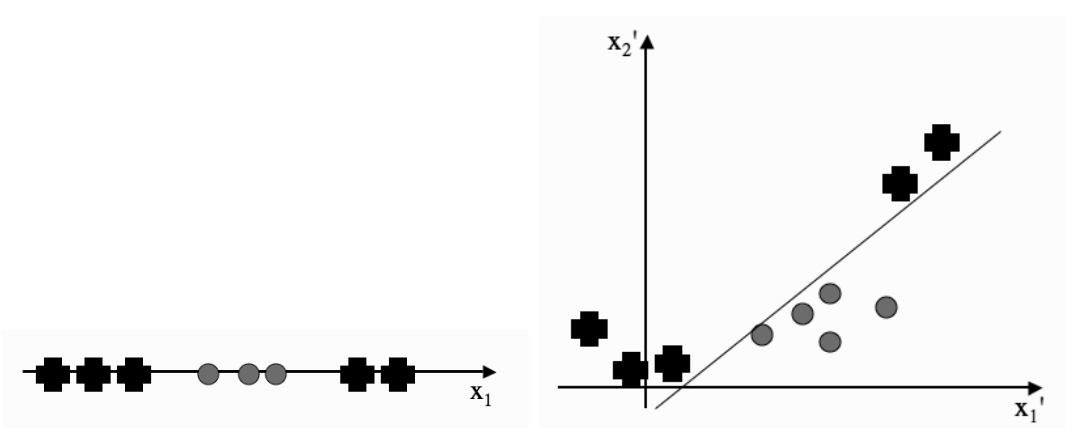
We let \(\phi_d(x) = x^d\), which linearly separates classes contained by other classes:
Explain why minimizing the norm of the vector of weights maximizes the margin